The Teaching of Mathematics in Basic Education of Russia in Zankov's perspective
Leonid Zankov (April 10 (23), 1901 – November 27, 1977), Academician, Doctor of Psychology, worked at the Institute of Theory and History of the Russian Academy of Pedagogical Sciences. He was a head of “The Laboratory of Social Education and Development” that it was renamed in 1968 into “The Laboratory for Problems of Teaching and Development of School Pupils”.
Leonid Zankov was among the first and closest disciples of Russian psichologist Lev Vygotsky (Vigotski). Lev Vygotsky studied the relationships between teaching, learning and child development and concluded that teaching and learning lead the child’s development. Vygotsky described an exceptionally important concept, the zone of proximal development. Zankov was first to test Vygotsky’s theories by conducting experimental research at Russia’s elementary schools. The aim was to determine the nature and degree of influence that teaching methods had on general development of primary grades’ students.
During the first stage of the experiment (1957-1961), a new system was created, and its principles were defined and embodied in concrete methods for the process of instruction and upbringing in the primary grades. In 1961, after new programs, methods, techniques and teaching materials had been created, the Laboratory began broad experiments.
The goal of elementary school education in Zankov’s system is general development of a child, which is the development of various sides of the child’s psyche. It includes intellect, will, and emotion. The significance of teaching derives from the fact that it creates the zone of proximal development, i.e., stimulates the child's interest in the environment which in turn awakens internal developmental processes.
In Zankov’s system, development is achieved through the realization of many components that constitute this system (Zankov, 1977). The directing and regulatory role in the system is played by its didactic principles. These principals are: 1) Teaching at an optimal level of difficulty. 2) Emphasizing theoretical knowledge. 3) Proceeding at a rapid pace. 4) Developing students’ awareness of the learning process. 5) The purposeful, systematic development of each student.
L. Zankov defined the main task of education as providing a child with the broad, integrated vision of the world by the means of science, art and direct knowledge. It is important to pay close attention to the construction of an educational process, the selection of the content, to the principles, technique and methods of teaching. It is important to provide careful attitude to the child's inner world – his/her age and individual characteristics, children's needs and interests. The material basis of the general development is the content, which consists of the facts and phenomena in their essential connections.
The goals of teaching mathematics are achieved in the process of understanding the connection between the need for description and explanation of the objects, processes, and phenomena in the surrounding world and the opportunity to do so, using quantitative and spatial relationships. The course of mathematics includes several directions: arithmetic, algebra, geometry and the history of mathematics.
During the lessons, students discover objectively existing relationships based on the notion of numbers. Recounting the number of items and denoting this number by digits, children are getting a meta-subject skill - counting.
237Numbers participate in actions; they present the results of measurements - length, mass, weight, area, size, capacity, time; express the dependencies between components in problems, etc.; the numbers help to characterize and construct geometric figures; to establish the properties of arithmetic operations, to introduce algebraic concepts: expression, equation, inequality. The history of mathematics and the origin of numbers gives the knowledge about modern and historical number systems, creates a vision of mathematics as a science.
| Grade 1 curriculum | Grade 2 curriculum |
|---|---|
| Why do people need mathematics? Comparison of the subjects How people learned to count and write the numbers Numbers and digits Number and digit 1 Number and digit 4 Number and digit 6 Equality Number and digit 9 Inequality Number and digit 5 Number and digit 3 Straight line Number and digit 2 Number and digit 7 Number and digit 8 Ray Segment Broken line The series of natural numbers and the number 0 History of counting Addition and subtraction Table of addition How people measured and are measuring the length Centimeter We compose and solve the problems Why letters of the Latin alphabet are used in mathematics Mathematical kaleidoscope Angles and polygons One-digit and two-digit numbers Mathematical kaleidoscope Addition with the transition through the tenth Subtraction with the transition through a dozen Mathematical kaleidoscope |
Mass and its measurement Check yourself Equations and their solutions Check yourself We compose and solve the problems Check yourself Addition and subtraction of two-digit numbers Capacity Time and its measurement Multiplication and division Check yourself Table of multiplication Check yourself Three-digit numbers Check yourself |
The lessons 2-4 are dedicated to the comparison of subjects according to their number, shape, colour, and size. Students learn that in comparison we always have to find first what is similar and then – what is different.

The objects can be compared by their numbers.
Where there are a lot of cherries – on the right tree or on the left tree?
Where there are a few cherries?
Compare the baskets. How are they similar? How are they different?
What else can we compare on this page using the words – a lot of, a few, more and less?

The objects can be compared by their shapes.
How many sandboxes are in the picture?
Compare the sandboxes on the top. How are they similar? How are they different?
In which sandbox there is a lot of sand?
Compare the sandboxes on the bottom according to their shapes and the amount of sand in each. Compare the sandboxes on the right. Compare the sandboxes on the left. How many round sandboxes are in the picture? How many square sandboxes are in the picture?
On what objects can you see the square, circle, triangle? Name these objects.
Draw as many circles in the notebook as there are round sandboxes, and as many squares as there are square sandboxes.
Through all exercises children compare, analyze, and make conclusions.
Exercise. Find similar lines.

Exercise. Where are there more squares – on the right or on the left?

Where are there less?
How many squares are on the right? How many are on the left?
Exercise. Compare these two figures.

Are they similar to each other? How the figure on the left is called?
How the figure on the right is called?
Eight exercises later: Compare these two figures. Are they similar?

How the first figure is called? How the second one is called?
10 exercises later: From these shapes choose two similar ones.

How similar are the chosen shapes? How different are they?
Why does the third shape not fit in with the two shapes you have chosen?
8 exercises later: compare two shapes.

In what way are they similar? In what way are they different?
Exercise. Compare the shapes. What are they called? Could one say that this is the same shape? Why not?

Exercise. Compare the shapes. How are they similar? How are they different?

What two shapes are more like each other than the other one?
How is the third shape different from the other two?
Exercise. Out of these three shapes, choose two that are similar.

How are they similar? How are they different? How is one figure different from the other two?
Exercise. Choose two similar shapes.

How similar are the chosen shapes? How different are they?
Why does the third shape not fit in with the chosen ones?
In the Zankov system’s mathematics curriculum there is a strong emphasis on geometry. Geometric properties of figures naturally appeal to the vivid imagination of young learners. All classroom work and exercises are directed toward establishing mathematical properties of geometric figures.
Exercise. Draw this figure in your notebook.

Count the number of squares. When counting, take into account squares of different sizes.
Later students are counting the squares in these figures.

Look carefully at the figure.

How many triangles are in it? Draw this figure.

Later.
Consider this figure.

How many triangles are in this figure?
In total, how many shapes are there? Sketch this figure in your notebook.
Copy this figure. How many triangles are in the figure? Record this number.
How many shapes are there in total? Record this number.
How many shapes are in this figure?

What shapes did you find?
Draw the same figure.
Copy this figure.

Write down how many triangles you found, how many quadrilaterals (quadrangles) you found, and how many shapes there are in total.
Beside the textbooks there are additional books for grade of 1 and 2 students. They are the notebooks "Mathematical games" (1st grade) and "Game material" (2nd grade). Tasks are designed to develop knowledge and skills on the main topics of the mathematics course, to exercise one’s attention and skills of observation.
Exercício.
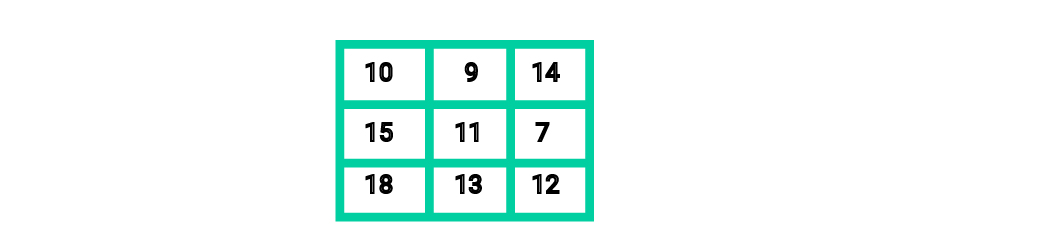
a) Write down sums of the numbers in each line of this square
b) Write down sums of the numbers in each column.
c) Write down sums of the numbers from corner to corner.
d) Calculate all written sums. What do you notice? Do you know how such a square is called? How would you call it? (In mathematics they are called magic squares).
e) Increase each number of this square by one and the same number. Check whether you get a magic square.
Exercise. a) Think, how to check if this square is magical:
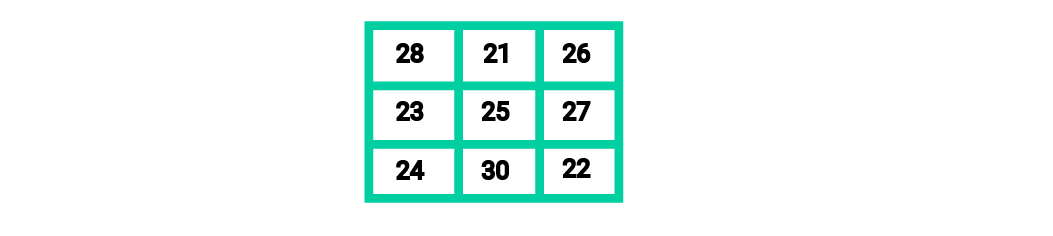
b) Is this method correct: one needs to sum up all the numbers in every row? Explain your answer. What do you think about this method: one needs to sum up all the numbers in every column?
c) Do all the necessary computations. What do you see? Did you need to find all sums to answer this question? Why?
d) Try to make this square magic. Explain how you did it. Exercise. a) Compose this figure:
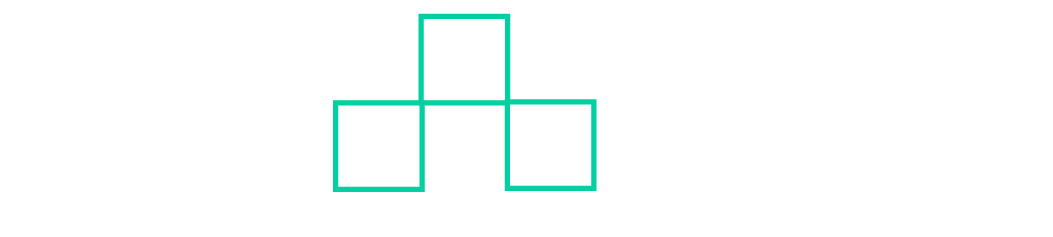
Replace 3 sticks in order to get 5 squares.
b) Draw this figure, point to the sticks you replaced, and draw the solution. Exercise. a) Construct the figure:

Move 4 sticks in order to get 5 squares.
b) Find different solutions. Draw the solutions.
Solving interesting problems, guessing puzzles and riddles, restoring and collecting unfamiliar pictures from details, students perform addition and subtraction within a hundred, repeat the tabulated cases of multiplication and division, determine the order of actions in expressions with two or three actions, i.e. in the game form, the computational skills necessary to assimilate the educational material are fixed.
The activities of the students themselves are the didactic centre of any class in Zankov’s system. The students not only solve and discuss various problems, but also observe, compare, group, classify, explain and arrive to conclusions. It is them who work with the material studied and transform it.
References
ARGINSKAIA, I. I.; BENENSON, E. P.; ITINA, L. S.; KORMISHINA, S. N. Mathematics. Grade 1. Samara: Fedorof, 2014.
ARGINSKAIA, I. I.; BENENSON, E. P.; ITINA, L. S.; KORMISHINA, S. N. Mathematics. Grade 2. Samara: Fedorof, 2014.
GUSEVA, L. G.; SOSNOWSKI, A. N. Russian education in transition: trends at the primary level. Canadian and International Education. 1997, v. 26, n. 1, p. 14-31. URL: http://ir.lib.uwo.ca/cie-eci/vol26/iss1/3
ZANKOV, L. V. et al. Teaching and development, New York: M.E. Sharpe Inc., 1977.
